Elementary Graphics with MS-Visual C v:1.52
by Richard D. Foerster
This tutorial focuses on development of an elementary set of drawing functions for use in MS-Dos Executable {.exe} Programs, using ANSI standard 'c' (rather than c++) wherever possible. Techniques used here rely on the graphics.lib that is included with version 1.52 of MS Visual C. Other versions of 'c' may be able to be adapted, using the generalized techniques discussed here. It should be understood that graphics pose an inherent limitation to portability of programs, even between similar system platforms. MSVC Version 5 is the current product. If this is the version you have you will need to compare the graph header and make adaptations if needed. Also, if you have relatively new hardware, your video display system may have new features that are incompatible with older standards. By experimentation, you need to determine the video modes that work with your system hardware. With this is mind you may have to experiment a little to identify the parameters, if any, that need to be changed.
The tutorial will be presented in number of parts to illustrate the overall steps that are used to develop the draw library from beginning concept to finished demonstration program, in the following five parts:
| 1 | Environment Considerations & Tests |
| 2 | Screen Coordinate System |
| 3 | Developing Drawing Algorithms |
| 4 | Development of a Prototype Program |
| 5 | Conversion to a Re-usable Library |
A natural starting point is the graph.h file, from which you can determine the video modes that are supported. You may want to consult doccumentation for your video card and monitor if it is available. Use Caution when experimenting, since selecting certain resolution modes can damage inappropriate monitors and video cards. Examination of the graph header file will also allow identifying data structures, functions and other tools that can be used by draw library routines. Two modes; _MAXRESMODE and _MAXCOLORMODE do not work with some newer video cards. Below is a list of the video modes {actually symbolic constants defined in graph.h} indicated in the v:1.52 header:
| _MAXRESMODE | -3 | _HERCMONO | 8 |
| _MAXCOLORMODE | -2 | _MRES16COLOR | 13 |
| _DEFAULTMODE | -1 | _HRES16COLOR | 14 |
| _ERESNOCOLOR | 15 | ||
| _TEXTBW40 | 0 | _ERESCOLOR | 16 |
| _TEXTC40 | 1 | _VRES2COLOR | 17 |
| _TEXTBW80 | 2 | _VRES16COLOR | 18 |
| _TEXTC80 | 3 | _MRES256COLOR | 19 |
| _MRES4COLOR | 4 | _ORESCOLOR | 64** |
| _MRESNOCOLOR | 5 | ** OLIVETTI ONLY | |
| _HIRESBW | 6 | ||
| _TEXTMONO | 7 |
In addition to video modes, you will discover that graphic.lib functions use a data structure _videoconfig to access and track video attributes. Structure members include:
| numxpixels | numypixels | numcolors |
| bitsperpixel | numvideopages | memory |
| mode | adapter | numtextcols |
| numtextrows |
The statement: struct _videoconfig vc; allows the structure members to be accessed by use of the dot operator, in the form: vc.numxpixels, for example.
A function _setvideomode() is available to be used to actually change the video from one mode to another. A companion function _getvideomode() allows a program to determine the attributes of the current video settings. To assure that the desired video mode has been set a conditional statement can be used to cause an error exit if the mode set operation is not successful. For example:
if
(!_setvideomode(_MAXCOLORMODE))
exit(1);
To illustrate the use of the graph header discoveries, you should examine the program source: vidck.c. This simple demonstration program calls the local function: TstDisplay() ( prototype: void TstDisplay(int Flg); ) with the integer value, represented by the symbolic constant, of the desired mode to be tested as the only argument. Eight common modes are selected, in turn, effectively testing the video attributes of the system on which it is being run. Any video mode that doesn't display, is not supported by the video display system. You can modify the list of modes or add more modes to suit your own needs.
The graph.h file shows that a number of graphic functions are available for use by programmers, however, the purpose of this tutorial is to demonstrate user developed graphic functions. It may be interesting to experiment with use of the functions that are included in the graphics.lib if you want to go farther.
Unlike most libraries, where the header and the library share the same filename, graph.h contains the prototypes, symbolic constants and other definitions used in graphics.lib. Reading near the front of graph.h you will uncover a technique for forcing the inclusion of a precompiled 'static library' in a project. Consider these lines:
#ifndef _WINDOWS
/* Force graphics.lib to be linked in if graph.h used */
#pragma comment(lib,"graphics.lib")
#endif
The comment #pragma places a comment record into an object or executable file. The keyword lib is one of 5 comment types that can be desiganted. It causes a library-search record to be placed in the object file. When used, it requires a commentstring perameter {"graphics.lib", for example} which causes the linker to search for the file indicated in the commentstring. The comment string can include the path.
Screen Coordinate System - Part 2The video display is arranged so that the upper left corner is designated as: 1,1 where x=1 and y=1. For a video mode that supports 640x480 resolution the lower right corner is designated as: 640,480 where x=640 and y = 480. the following diagram illustrates this.
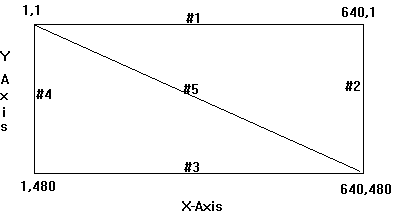
In the diagram above five lines are drawn. Each can be represented by the following:
| 1 | 1,1 640,1 | x1=1, y1=1 x2=640 y2=1 | Zero Slope |
| 2 | 640,1 640,480 | x1=640, y1=1 x2=640, y2=480 | NO SLOPE |
| 3 | 1,480 640,480 | x1=1, y1=480, x2=640, y2=480 | Zero Slope |
| 4 | 1,1 1,480 | x1=1, y1=1, x2=1, y2=480 | NO SLOPE |
| 5 | 1,1 640,480 | x1=1, y1=1, x2= 640, y2=480 | Non-Vert Line |
Back to Selector Development of Drawing Algorithms - Part 3Development of Drawing Algorithms - Part 3
You may recall from Algebra that any non-vertical line {#1,3, or 5} is uniquely determined by an attribute called slope and the point at which it intercepts the y-axis. Vertical lines must be detected and dealt with separately. To see how this works, consider this example based on line #5, above. The slope, which you can think of as the slant of the line, can be determined by the formula:
m = (y2 - y1) / (x2 - x1)where: m is the slope and y2 is the end point of y and y1 is the start point of y. Furthermore, x2 is the end point of x and x1 is the beginning point of x.
Using this formula we can determine the slope of line #5 as:
m = (480 - 1) / (640 - 1) or 479/639 then ..... m = 0.7496
Now a variation of the slope-intercept equation {y = mx + b} can be used to determine the offset required to start the line at the beginning y coordinate. The formula we need, can be derived algebraically to solve for the offset value {b}, and it is:
b = (m * x1 - y1) * -1 or b = (.7496 * 1 - 1) * (-1) then... b = 0.2504
Finally we can calculate y for any point of x using the standard slope-intercept equation as follows:
y = mx + b or if x = 1...... 0.7496 * 1 + 0.2504 = 1 andif x = 640.... 0.7496 * 640 + 0.2504 = 479.94 {or 480}
thus: 1,1 640,480 describes line #5 in this example.
In a horizontal line, the change of y for each point x is 0. Line #1 {1,1, 640,1} and #3 {1,480 640,480} are horizontal lines that illustrate this fact, since you will quickly observe that y2 - y1 is zero in both instances.
Considering line #1 the consequence of ZERO Slope is as follows:
b = (0 * 1 - 1) * (-1) or (-1) * (-1) which = 1
then....
y = 0 * 1 + 1 then y = 1 so that y = 1 {or y1} for all values of x
Observe that in the case of line 3 the start value of y {y1} is 480 so that:
b = (0 * 1 - 480) * (-1) or (-480) * (-1) which
= 480 then....
y = 0 * 1 + 480 then y = 480 so that y = 480 {or y1} for all values of x
Thus a horizontal line {zero slope} works with our formulas and does not cause a problem. As a consequence, it is not necessary to treat the zero slope case as a special condition. Since y is constant in this case, there is no need to calculate it. Furthermore, calculation of the offset {b} is meaningless, so that the addition of a few lines of code to test for this case will produce a more efficient program.
A vertical line {NO SLOPE} is a different matter. In a vertical line the change in x for any point y is 0. Line #2 {640,1 , 640, 480} and line #4 {1, 1, 1, 480} illustrate this since x2-x1 = 0 in both cases. However, if we apply these coordinates to determine the slope of our line a divide by zero error will occur. For example in the case of line #2 :
m = (y2 - y1) / (x2 - x1) then.... m = (480 - 1) / (640 - 640) or 479 / 0
To solve this problem, all that needs to be done is to test to see if the no-slope condition exists. This is done by checking to see if x2 - x1 = 0. If so, x can be set to the constant value of x1. Remember in the no-slope case x does not change for any value of y. With x determined, we need only generate y-values for y1 to y2 to describe the line.
One final condition exists, and that is the case where the coordinates refer to a single point. In this case both y2-y1 and x2-x1 are zero. For example the line 100,200 100,200 is the single point case. Therefore the program needs to test for three conditions: x2-x1 zero, y2-y1 zero, and both y2-y1 and x2-x1 zero.Back to Selector Development of a prototype program - Part 4
A re-usable routine to draw a line on the screen by simply passing the desired screen coordinates would be a useful start to set of custom drawing tools. Re-examining the graph.h provides the information we need. In particular a function {prototype: _setpixel(short, short); } is available to set {draw} an individual pixel when the x,y coordinate pair is provided. In addition a function {prototype: _setcolor(short); } can be used to specify the color of a line before it is drawn. As in the earlier example, using the data structure {struct _videoconfig vc; } will allow the resolution of the display to be determined by accessing structure members The function: _getvideoconfig(&vc); is used to load current display settings to the structure.
With the video resolution known, it is possible to test the generated y values and x values to assure that they don't exceed the limits of the display. Structure members numypixels and numxpixels can be used used for this test.
In this part of the tutorial you should carefully examine the example program pix2.c that is included in the download packet. The line function being developed is based on the prototype:
int line( short sx, short sy,short ex, short ey, short color );The parameter list notation is: sx=start x, sy=start y, ex=end x, ey=end y, and color. All parameters are of type short integer since this is the type that must be passed to the graph.h functions. An integer returned by the function allows the calling program to detect errors {-1 for display limit errors} and/or a single point condition {-99} or a normal exit which is indicated as zero.
On entry to the line function, the current video configuration must be obtained, using _getvideoconfig(). Local variables ts1 and ts2 are used to determine the value of ey-sy and ex-sx, respectively. The results are then tested to determine special cases. If the case is a single point set the color, then set the pixel and return -99 value. If ts1 = 0 {zero slope} then the variable slpe is set equal to 0. If ts2 = 0 {the NO SLOPE condition} then the variable slpe is set to 9999, otherwise {t2 <> 0} then the value of slpe is calculated.
For the NO SLOPE case {vertical Line} x is always equal to sx, since sx=ex, for all values of y. All is that is needed is to generate y values from sy to ey and use the _setpixel() for each.
For all remaining cases {ZERO SLOPE and all non-vertical lines} the offset b must be calculated. Then y can be calculated for each value of x from sx to ex.
Once the requirements of the line function have been identified and coded, a simple main() can be written to test line(). First, the screen resolution should be set if other than _DEFAULTMODE is needed. This can be accomplished following the convention used earlier. For this example the mode is set to _VRES16COLOR). The user then has the opportunity to enter the color {1-16} for the line, with the value -99 used to break out of the infinite loop. Next, the user enters values for sx,sy, ex, ey separated by spaces only -- NO COMMAS!
These values are then adjusted for base zero, and passed as arguments to the line function. Before exiting, the program must restore the video configuration by: _setvideomode(_DEFAULTMODE).
Once the line() has been tested, it is hard to resist the urge to implement a box() function which uses only horizontal and vertical lines. Similar to line(), the box function is based on the prototype:
int box( short ulx, short uly, short lrx, short lry, short color)In this instance, ulx indicates the upper left corner x-value, and uly indicates the upper left corner y-value. Similarly, lrx indicates the lower right corner x, and ury indicates the lower right corner y-value. Permutations of the sx,sy ex,ey coordinates are all that needed to produce a box made up from 4 lines. The perameter list could have used the same naming conventions used in line(). Using the notion of Upper left x,y and Lower right x,y helps the user to visualize the coordinates more easily. Note, however that the naming convention has no effect on the actual entry of coordinates, since the order is identical in both line() and box().
A calling program can call box() directly, but in this demo, when the user enters -99 to stop entering line coordinates, a box is drawn based on the last entered coordinates.
Using similar techniques, other shapes, such as a triangle could be created, calling the line function to perform the drawing, but this challenge is left up to the student for implementation.Back to Selector Conversion to a Re-usable Library & Documentation
Part 5
Once the test program has been completed, the line() and box() routines can be converted to become an initial draw library {drawLib}. Carefully compare the source files: draw.c, drawLib.h, and drawLib.c with the program {pix2.c} developed in part 4 for the following discussion.
The function prototypes for line() and box() are cut and pasted into a new file that will be saved as DrawLib.h. Next the actual line() and box() functions are cut and pasted into a new file that will be saved as DrawLib.c. This leaves the test program with only a main() which should be saved as Draw.c. To test the program and sub-modules, create a new .MAK and be sure to list Draw.c and DrawLib.c, and any other libraries needed in the list of included files. Finally build and test to make sure all elements are correct and complete.
To Examine the source files that make up the example programs, included in this tutorial: first, Download the turotial source code and Demo programs which include:
| vidck.c | The video mode checking program |
| graph.h | The MSVC v:1.52 graphic header file |
| pix.mak | Project .MAK for preliminary EXAMPLE |
| Pix2.c | Preliminary EXAMPLE program. Derived from it are: |
| draw.c | Example Test program source code file |
| drawLib.h | The Header containing prototypes for line() and box() |
| drawLib.c | The Draw Library functions source code file |
| draw.mak | The Library Module Example project .MAK |
.exe files are ready to run programs
produced by the corresponding source.